Data Encryption Standard

Introduce and cryptanalysis DES

Posted Dec 31, 2024

By Dang Minh Tu

16 min read

Introduce

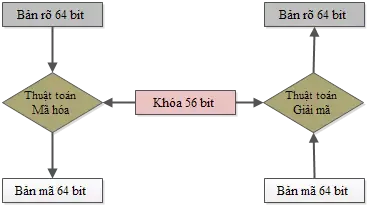
Data Encryption Standard (DES) là chuẩn mã hóa dữ liệu đầu tiên trên thế giới, do Cơ quan an ninh mạng Quốc gia Hoa Kỳ (NSA) đề xuất trên cơ sở cải tiến thuật toán Lucifer do hãng IBM công bố năm 1964.

Đầu vào của DES là khối 64-bit, đầu ra cũng là khối 64-bit. Khóa mã hóa có độ dài 56-bit, nhưng thực chất ban đầu là 64-bit, được lấy đi các bit ở vị trí chia hết cho 8 dùng để kiểm tra tính chẵn lẻ.

Algorithm

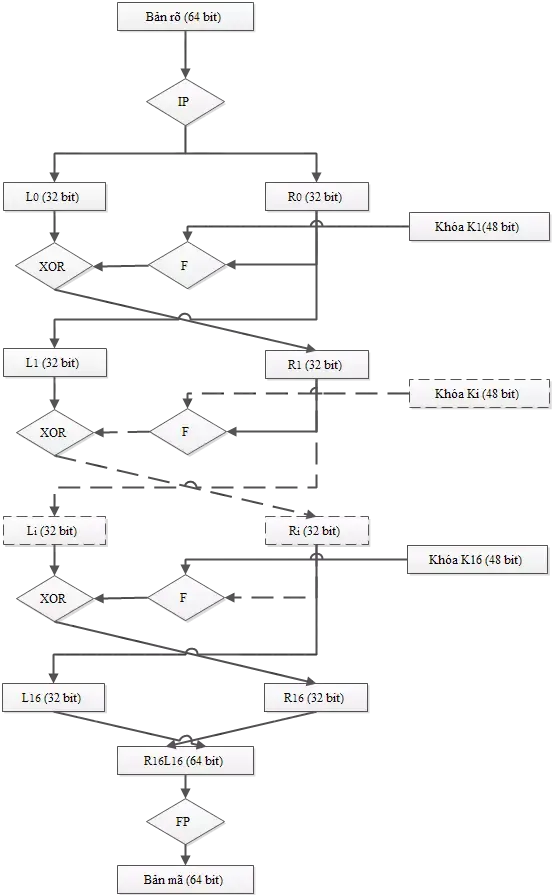
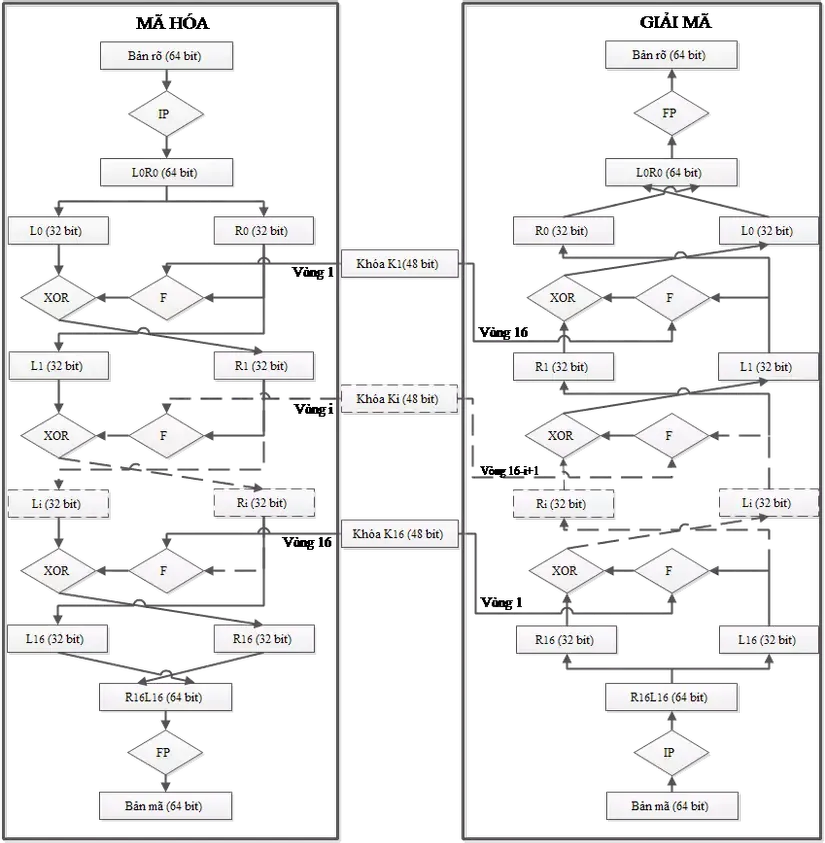
DES là thuật toán mã hóa theo khối, nó xử lý từng khối thông tin của bản rõ có độ dài xác định là 64-bit. Trước khi đi vào 16 chu trình chính, khối dữ liệu cần bảo mật sẽ được tác ra từng khối 64-bit, từng khối này sẽ lần lượt được đưa vào 16 vòng mã hóa DES để thực hiện.

Bước 1: Sinh khóa con: sử dụng thuật toán sinh khóa con từ khóa K ta sẽ được 16 khóa con K1, K2, ..., K16.
Bước 2: Sử dụng phép hoán vị khởi đầu Initial Permutation (IP) để hoán vị các bit của bản rõ M . Kết quả nhận được chia thành 2 nửa là $L_0 = m_{63}m_{62}…m_{32}, \ R_0 = m_{31}m_{30}…m_0.$
Bước 3: Với i chạy từ 1 → 16 thực hiện: tính các $\text{L}_i$ và $\text{R}_i$ theo công thức:

\[\text{L}_i = \text{R}_{i-1}, \ \ \ \text{R}_i = \text{L}_{i-1} \oplus \text{f}(\text{R}_{i-1}, \text{K}_i)\]

trong đó, $f(R_{i-1}, K_i) = R(S(E(R_{i-1}) \oplus K_i))$ (phần này sẽ được trình bày chi tiết sau).

Bước 4: đổi vị trí khối $L_{16}, R_{16}$ ta được $L_{16}R_{16} = b_0b_1…b_{63}.$
Bước 5: Sử dụng phép hoán vị kết thúc Final Permutation (FP) - nghịch đảo với hoán vị khởi đầu IP, ta thu được bản mã cần tìm: $\text{C} = \text{IP}^{-1}(b_0b_1…b_{63}).$

Gen subkey

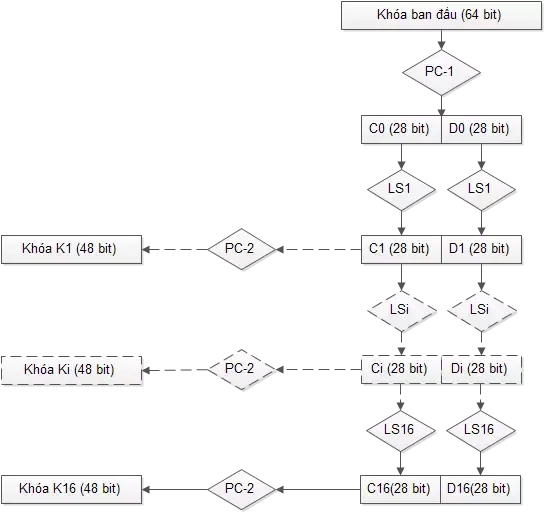
16 vòng lặp của DES chạy cùng thuật toán như nhau nhưng với 16 khóa con khác nhau. Các khóa con đều được sinh ra từ khóa chính của DES bằng thuật toán sinh khóa con.

Khóa ban đầu là 1 xâu có độ dài 64-bit, bit thứ 8 của mỗi byte sẽ được lấy ra để kiểm tra phát hiện lỗi, tạo ra chuỗi 56-bit. Sau khi bỏ các bit kiểm tra ta sẽ hoán vị chuỗi 56-bit này. Hai bước trên được thực hiện thông qua hoán vị ma trận PC-1 (Permuted choice 1).

  
# Permutation Choice 1
PC1 = [57, 49, 41, 33, 25, 17, 9,
        1, 58, 50, 42, 34, 26, 18,
        10, 2, 59, 51, 43, 35, 27,
        19, 11, 3, 60, 52, 44, 36,
        63, 55, 47, 39, 31, 23, 15,
        7, 62, 54, 46, 38, 30, 22,
        14, 6, 61, 53, 45, 37, 29,
        21, 13, 5, 28, 20, 12, 4]

Tiếp theo ta chia kết quả sau khi PC-1 thành 2 phần: C0 = 28 bit đầu và D0 = 28 bit cuối . Mỗi phần này sẽ được xử lý 1 cách độc lập. $C_i = LS_i(C_{i-1}), \ \ D_i = LS_i(D_{i-1})$. Trong đó $LS_i$ là phép dịch bit vòng sang sái (left shift) 1 hoặc 2 vị trí tùy thuộc vào i.

  
LEFT_ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]

Cuối cùng sử dụng hoán vị cố định PC-2 (Permuted choice 2) để hoán vị chuỗi $C_iD_i$ 56-bit thành khóa $K_i$ với 48-bit.

  
# Permutation Choice 2
PC2 = [14, 17, 11, 24, 1, 5, 3, 28,
        15, 6, 21, 10, 23, 19, 12, 4,
        26, 8, 16, 7, 27, 20, 13, 2,
        41, 52, 31, 37, 47, 55, 30, 40,
        51, 45, 33, 48, 44, 49, 39, 56,
        34, 53, 46, 42, 50, 36, 29, 32]

Encryption

Với bản rõ cho trước x, 1 xâu x' sẽ được tạo ra bằng cách hoán vị các bit của x theo hoán vị ban đầu Initial Permutation (IP).

  
# Initial Permutation table
    IP = [58, 50, 42, 34, 26, 18, 10, 2,
          60, 52, 44, 36, 28, 20, 12, 4,
          62, 54, 46, 38, 30, 22, 14, 6,
          64, 56, 48, 40, 32, 24, 16, 8,
          57, 49, 41, 33, 25, 17, 9, 1,
          59, 51, 43, 35, 27, 19, 11, 3,
          61, 53, 45, 37, 29, 21, 13, 5,
          63, 55, 47, 39, 31, 23, 15, 7]

    def initial_permutation(self, block):
        return self.permute(block, self.IP)

Tiếp theo x' sẽ được chia thành 2 phần L0, R0 , trong đó L0 = 32 bit đầu và R0 = 32 bit đầu .

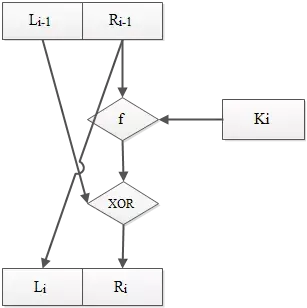
Tính toán 16 lần bằng 1 hàm xác định. Ta sẽ tính theo quy tắc:

\[L_i = R_{i-1}, \ \ \ R_i = L_{i-1} \oplus f(R_{i-1},K_i)\]

Với $K_i$ là khóa được sinh ra ở quá trình tạo khóa, $f$ là một hàm sẽ được trình bày ở sau.

Sau đó áp dụng hoán vị kết thúc Final Permutation (FP) cho xâu bit $R_{16}L_{16}$ ta thu được bản mã y .

  
# Final Permutation table (Inverse Initial Permutation)
FP = [40, 8, 48, 16, 56, 24, 64, 32,
       39, 7, 47, 15, 55, 23, 63, 31,
       38, 6, 46, 14, 54, 22, 62, 30,
       37, 5, 45, 13, 53, 21, 61, 29,
       36, 4, 44, 12, 52, 20, 60, 28,
       35, 3, 43, 11, 51, 19, 59, 27,
       34, 2, 42, 10, 50, 18, 58, 26,
       33, 1, 41, 9, 49, 17, 57, 25]
def final_permutation(self, block):
    return self.permute(block, self.FP)

Decryption

Quá trình giải mã của DES cũng tương tự quá trình mã hóa. Chỉ khác nhau ở:

\[L_i = R_{i-1}, \ \ \ R_i = L_{i-1} \oplus f(R_{i-1}, K_{16-i+1})\]

Như vậy khóa K của hàm f sẽ đi từ 16 → 1.

F function

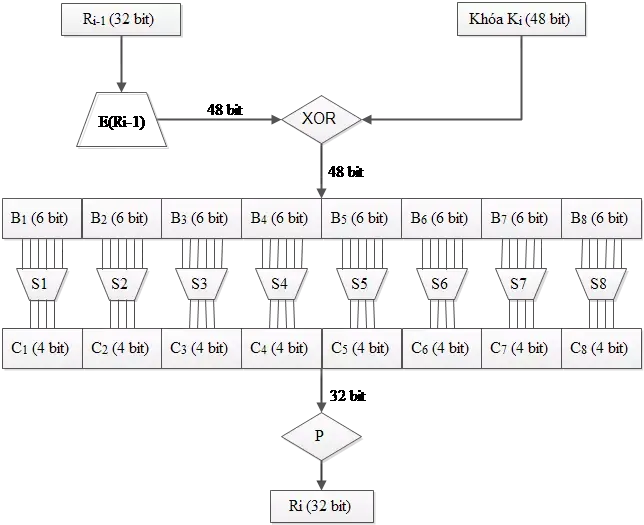
Đầu vào hàm $f$ có 2 biến:

Biến thứ nhất: $R_{i-1}$ là xâu có độ dài 32-bit.
Biến thứ hai: $K_i$ là xâu bit có độ dài 48-bit.

Đầu ra của hàm $f$ là xâu 32-bit.

Quy trình hoạt động như sau:

Biến thứ nhất $R_{i-1}$ được mở rộng thành một xâu có độ dài 48-bit theo hàm mở rộng hoán vị Expansion Permutation (E).
Tính $E(R_{i-1}) \oplus K_i$ .
Tách kết quả của phép tính trên thành 8 xâu 6 bit $B_1, B_2, …, B_8$.
Đưa cá khối 6-bit $B_i$ vào 8 bảng $S_1, S_2,…,S_8$ (sbox). Mỗi $S_i$ là một bảng 4x16 cố định có các cột từ 0 → 15 và các hàng từ 0 → 3. Với mỗi xâu 6-bit $B_i = b_1b_2b_3b_4b_5b_6$ ta tính $S_iB_i$ như sau: hai bit $b_1b_6$ xác định hàng r trong $S_i$, bốn bit $b_2b_3b_4b_5$ xác định cột c trong $S_i$. Khi đó, $S_i(B_i)$ sẽ xác định phần tử $C_i = S_i(r, c)$, phần tử này viết dưới dạng nhị phân 4-bit. Như vậy, 8 khối 6-bit $B_i$ sẽ cho ra 8 khối 4-bit $C_i$.
Xâu bit $C = C_1C_2C_3C_4C_5C_6C_7C_8$ có độ dài 32-bit được hoán vị theo phép toán hoán vị P . Kết quả của P(C) sẽ là kết quả của hàm $f$.

Full script DES encryption and decryption:

  
# -*- coding: utf-8 -*-
class DES:
    # Initial permutation table
    # Permutation Choice 1
    PC1 = [57, 49, 41, 33, 25, 17, 9,
           1, 58, 50, 42, 34, 26, 18,
           10, 2, 59, 51, 43, 35, 27,
           19, 11, 3, 60, 52, 44, 36,
           63, 55, 47, 39, 31, 23, 15,
           7, 62, 54, 46, 38, 30, 22,
           14, 6, 61, 53, 45, 37, 29,
           21, 13, 5, 28, 20, 12, 4]

    # Permutation Choice 2
    PC2 = [14, 17, 11, 24, 1, 5, 3, 28,
           15, 6, 21, 10, 23, 19, 12, 4,
           26, 8, 16, 7, 27, 20, 13, 2,
           41, 52, 31, 37, 47, 55, 30, 40,
           51, 45, 33, 48, 44, 49, 39, 56,
           34, 53, 46, 42, 50, 36, 29, 32]

    def permute(self, data, table):
        return ''.join(data[i-1] for i in table)

    # Left rotations for each round
    LEFT_ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]

    def left_rotate(self, data, shifts):
        return data[shifts:] + data[:shifts]

    def __init__(self, key):
        self.key = key
        self.subkeys = self.generate_subkeys(key)

    def generate_subkeys(self, key):
        # Apply PC-1 permutation on the key
        key_56bit = self.permute(key, self.PC1)

        # Split the key into two 28-bit halves
        left_half = key_56bit[:28]
        right_half = key_56bit[28:]
        subkeys = []

        # Generate 16 subkeys
        for i in range(16):
            # Left rotate both halves
            left_half = self.left_rotate(left_half, self.LEFT_ROTATIONS[i])
            right_half = self.left_rotate(right_half, self.LEFT_ROTATIONS[i])

            # Combine the halves and apply PC-2 permutation
            combined_key = left_half + right_half
            subkey = self.permute(combined_key, self.PC2)
            subkeys.append(subkey)

        return subkeys

    ######################Initial permutation
    # Initial Permutation table
    IP = [58, 50, 42, 34, 26, 18, 10, 2,
          60, 52, 44, 36, 28, 20, 12, 4,
          62, 54, 46, 38, 30, 22, 14, 6,
          64, 56, 48, 40, 32, 24, 16, 8,
          57, 49, 41, 33, 25, 17, 9, 1,
          59, 51, 43, 35, 27, 19, 11, 3,
          61, 53, 45, 37, 29, 21, 13, 5,
          63, 55, 47, 39, 31, 23, 15, 7]

    def initial_permutation(self, block):
        return self.permute(block, self.IP)
    #################### Inverse Initial Permutation
    # Final Permutation table (Inverse Initial Permutation)
    FP = [40, 8, 48, 16, 56, 24, 64, 32,
          39, 7, 47, 15, 55, 23, 63, 31,
          38, 6, 46, 14, 54, 22, 62, 30,
          37, 5, 45, 13, 53, 21, 61, 29,
          36, 4, 44, 12, 52, 20, 60, 28,
          35, 3, 43, 11, 51, 19, 59, 27,
          34, 2, 42, 10, 50, 18, 58, 26,
          33, 1, 41, 9, 49, 17, 57, 25]

    def final_permutation(self, block):
        return self.permute(block, self.FP)

    #####################Expansion table 32 bits to 48 bits
    # Expansion table
    E = [32, 1, 2, 3, 4, 5,
         4, 5, 6, 7, 8, 9,
         8, 9, 10, 11, 12, 13,
         12, 13, 14, 15, 16, 17,
         16, 17, 18, 19, 20, 21,
         20, 21, 22, 23, 24, 25,
         24, 25, 26, 27, 28, 29,
         28, 29, 30, 31, 32, 1]

    ###################### Substution Phases

    # S-boxes
    S = [
        # S1
        [
            [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
            [0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
            [4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
            [15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]
        ],
        #S2
        [
            [15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
            [3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
            [0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
            [13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],
        ],

        #S3
        [
            [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
            [13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
            [13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
            [1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],
        ],

        #S4
        [
            [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
            [13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
            [10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
            [3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
        ],

        #S5
        [
            [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
            [14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
            [4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
            [11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],
        ],

        #S6
        [
            [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
            [10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
            [9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
            [4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],
        ],

        #S7
        [
            [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
            [13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
            [1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
            [6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],
        ],

        #S8
        [
            [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
            [1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
            [7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
            [2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
        ]
    ]

    def sbox_substitution(self, block):
        substituted = ""
        for i in range(8):
            chunk = block[i*6:i*6+6]
            row = int(chunk[0] + chunk[5], 2)
            col = int(chunk[1:5], 2)
            substituted += format(self.S[i][row][col], '04b')
        return substituted
    #####################Expansion table 32 bits to 48 bits
    # Expansion table
    E = [32, 1, 2, 3, 4, 5,
         4, 5, 6, 7, 8, 9,
         8, 9, 10, 11, 12, 13,
         12, 13, 14, 15, 16, 17,
         16, 17, 18, 19, 20, 21,
         20, 21, 22, 23, 24, 25,
         24, 25, 26, 27, 28, 29,
         28, 29, 30, 31, 32, 1]

    def expand(self, block):
        return self.permute(block, self.E)

    ###################### Feistel Function f()
    # Permutation table for the Feistel function
    P = [16, 7, 20, 21, 29, 12, 28, 17,
         1, 15, 23, 26, 5, 18, 31, 10,
         2, 8, 24, 14, 32, 27, 3, 9,
         19, 13, 30, 6, 22, 11, 4, 25]

    def feistel_function(self, block, subkey):
        # Step 1: Expansion
        expanded_block = self.expand(block)

        # Step 2: Subkey Mixing
        mixed_block = self.xor(expanded_block, subkey)

        # Step 3: S-box Substitution
        substituted_block = self.sbox_substitution(mixed_block)

        # Step 4: Permutation
        permuted_block = self.permute(substituted_block, self.P)

        return permuted_block

    def xor(self, block1, block2):
        return ''.join(['1' if b1 != b2 else '0' for b1, b2 in zip(block1, block2)])

    ##################Encryption one block (64 bits)
    def encrypt(self, plaintext):
        # Step 1: Initial Permutation
        permuted_block = self.initial_permutation(plaintext)

        # Split the block into left and right halves
        L, R = permuted_block[:32], permuted_block[32:]

        # Step 2: 16 Rounds of Processing
        for i in range(16):
            new_R = self.xor(L, self.feistel_function(R, self.subkeys[i]))
            L, R = R, new_R

        combined_block = R + L

        # Step 3: Final Permutation
        ciphertext = self.final_permutation(combined_block)

        return ciphertext
    ##################Decryption one block (64 bits)
    def decrypt(self, ciphertext):
        # Step 1: Initial Permutation
        permuted_block = self.initial_permutation(ciphertext)

        # Split the block into left and right halves
        L, R = permuted_block[:32], permuted_block[32:]

        # Step 2: 16 Rounds of Processing (starting from the last subkey)
        for i in range(15, -1, -1):
            new_R = self.xor(L, self.feistel_function(R, self.subkeys[i]))
            L, R = R, new_R

        combined_block = R + L

        # Step 3: Final Permutation
        plaintext = self.final_permutation(combined_block)

        return plaintext

# Usage:  DES mode ECB
from Crypto.Util.Padding import pad, unpad

def bytes_to_bin(data: bytes) -> str:
    return ''.join(format(b, '08b') for b in data)

def bin_to_bytes(bits: str) -> bytes:
    return int(bits, 2).to_bytes(len(bits)//8, 'big')

plaintext = pad(b'dangminh', 8)
key = b'12345678'

binary_plaintext = bytes_to_bin(plaintext)
binary_key = bytes_to_bin(key)

ciphertext = b""
for i in range(0, len(binary_plaintext), 64):
    block = binary_plaintext[i:i+64]
    des = DES(binary_key)
    encrypted_block = des.encrypt(block)
    ciphertext += bin_to_bytes(encrypted_block)

print("Ciphertext (hex):", ciphertext.hex())

binary_ciphertext = bytes_to_bin(ciphertext)
decrypted_text = b""
for i in range(0, len(binary_ciphertext), 64):
    block = binary_ciphertext[i:i+64]
    des = DES(binary_key)
    decrypted_block = des.decrypt(block)
    decrypted_text += bin_to_bytes(decrypted_block)

print("Decrypted text:", decrypted_text)

Cryptography

DES

This post is licensed under CC BY 4.0 by the author.