Cryptanalysis of Stream Ciphers

Introduce to stream ciphers and cryptanalysis it

Posted Sep 24, 2025

By Dang Minh Tu

17 min read

RC4

Introduce

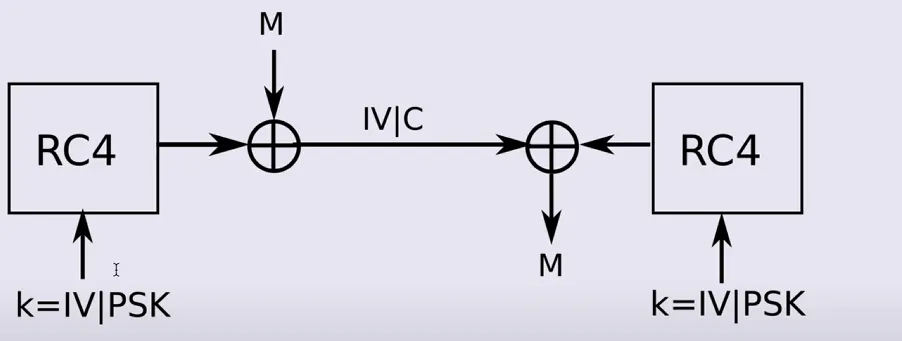
RC4 là một loại mã hóa dòng (stream cipher). Nó tạo ra keystream từ secret keybằng 2 thuật toán Key Scheduling Algorithm (KSA) và Pseudo Random Generation Algorithm (PRGA).

Sau đó tính ciphertext = plaintext XOR keystream .

Chi tiết về 2 giai đoạn chính trong RC4:

Key Scheduling Algorithm

Giai đoạn này sẽ tạo ra một hoán vị ban đầu của mảng trạng thái S. Ở đây, S là mảng 256 bytes, chứa các giá trị từ 0 → 255.

Thuật toán:

Khởi tạo S = [0, 1, 2, ..., 255].
Dùng secret key K để làm xáo trộn S.
Biến đổi S bằng vòng lặp 256 bước:
- j = (j + S[i] + K[i % keylen]) % 256.
- Swap S[i] và S[j].

Code:

  
def rc4_ksa(key: bytes):
    keylen = len(key)
    S = list(range(256))
    j = 0
    for i in range(256):
        j = (j + S[i] + key[i % keylen]) & 0xFF
        S[i], S[j] = S[j], S[i]
    return S

Pseudo Random Generation Algorithm

PRGA dùng mảng trạng thái S (đã qua bước KSA) để liên tục tráo đổi và sinh ra các byte giả ngẫu nhiên. Mỗi vòng lặp của PRGA sinh ra 1 byte keystream. Giai đoạn này sẽ được thiết kế sao cho S luôn được thay đổi sau mỗi vòng và keystream khó đoán được nếu không biết secret key.

Thuật toán:

Khởi tạo i = j = 0.
Với mỗi byte cần sinh:
- i = (i + 1) % 256 và j = (j + S[i]) % 256.
- Swap S[i] và S[j].
- Byte được trả về sẽ là: S[(S[i] + S[j]) % 256]

Code:

  
def rc4_prga(S):
    i, j = 0, 0
    while True:
        i = (i + 1) & 0xFF
        j = (j + S[i]) & 0xFF
        S[i], S[j] = S[j], S[i]
        K = S[(S[i] + S[j]) & 0xFF]
        yield K

Sơ đồ mã hóa của RC4:

Kết hợp cả 2 phần lại ta có full code encrypt RC4:

  
# rc4.py - Simple RC4 (KSA + PRGA)
def rc4_ksa(key: bytes):
    keylen = len(key)
    S = list(range(256))
    j = 0
    for i in range(256):
        j = (j + S[i] + key[i % keylen]) & 0xFF
        S[i], S[j] = S[j], S[i]
    return S

def rc4_prga(S):
    i, j = 0, 0
    while True:
        i = (i + 1) & 0xFF
        j = (j + S[i]) & 0xFF
        S[i], S[j] = S[j], S[i]
        K = S[(S[i] + S[j]) & 0xFF]
        yield K

def rc4_stream(key: bytes, data: bytes) -> bytes:
    S = rc4_ksa(list(key))
    gen = rc4_prga(S)
    out = bytearray(len(data))
    for idx, b in enumerate(data):
        out[idx] = b ^ next(gen)
    return bytes(out)

# Usage:
# key = b"secret"
# plaintext = b"Hello world"
# ciphertext = rc4_stream(key, plaintext)
# recovered = rc4_stream(key, ciphertext)   # same op recovers plaintext

Cryptanalysis

RC4 không định nghĩa nonce (IV ) cố định. Nó chỉ nhận secret key để tạo ra keystream , việc dùng nonce / IV là do protocol bao bọc RC4 quyết định.

KSA-based attacks (FMS attack)

Cuộc tấn công FMS trên RC4 này tận dụng các sai lệch thống kê trong dãy số ngẫu nhiên được tạo bởi RC4 để khôi phục lại khóa bí mật. FMS attack lần đầu được giới thiệu vào năm 2001. Nó làm nổi bật những lỗ hổng đáng kể trong RC4, đặc biệt là trong ngữ cảnh của các mạng không dây sử dụng giao thức WEP (Wired Equivalent Privacy).
Có rất nhiều biểu diễn của RC4 chọn key = IV + secret , ta sẽ chọn một trong những weak IV là (A + 3, 255, x) với A là byte của secret mà ta muốn khai thác.

Chi tiết thuật toán:

Ở hàm KSA, giả sử i = L :
- → $j_{L+1} = j_L + S_L[L] + \text{key}[L]$
- → $\text{key}[L] = j_{L+1} - j_L - S_L[L]$ $(*)$
Mình sẽ giải thích tại sao với weak IV như vậy thì ta có thể recover lại key (giả sử muốn tìm key[3] -> A = 0 -> IV = [3, 255, x] ):
- Round đầu tiên của KSA:
- Round thứ 2:
- Round thứ 3:
- Round thứ 4:
- Ta có sau 4 round thì mảng S hiện tại như thế này:
Note: với các giá trị x khác nhau, có khoảng 5% sau khi kết thúc KSA thì 2 vị trí đầu tiên sẽ là S[0] = A + 3, S[1] = 0 không bị thay đổi vị trí.
Khi đó, có khoảng 5% các giá trị x thì: $Q = j_{L+1}$
Từ $(*)$ suy ra: $\text{key}[L] = j_{L+1} - j_L - S_L[L] = Q - j_L - S_L[L]$
Cùng xem trong hàm PRGA, byte đầu tiên của keystream sẽ được mã hóa như thế nào.
Ồ, vậy keystream[0] là giá trị Q mà ta cần tìm. Khi đó ta đã có thể recover lại được key[L] .
Với phân bố hoàn toàn ngẫu nhiên không có bias, ta mong đợi $p_0 = \frac{1}{256}$ (với $p$ là xác suất ứng viên cho một weak IV cho ra đúng giá trị byte khóa. Nhưng trong trường hợp này lại có đến 5% giá trị x thì 2 vị trí đầu tiên sẽ có giá trị như vậy, từ đó ta thống kê với mỗi trường hợp x xem là key[L] nào xuất hiện nhiều nhất và xác định đó là giá trị cần tìm.

Code:

  
**secret_decr = []
sl = len(secret) # assume you know the secret length
for A in range(sl):
    probs = [0] * 256 # init a frequency array
    for v in range(256): # for each custom byte
        plaintext = b'A' * (A + 3) # doesn't matter the plaintext
        nonce = bytes([A+3, 255, v]) # weak nonce (L, n-1, v)

        ciphertext = ARC4.new(nonce + secret).encrypt(plaintext) # this line is send to the oracle and we receive the ciphertext

        keystream = xor(plaintext, ciphertext) # compute the keystream

        # simulate first known rounds to get j
        key = nonce + bytes(secret_decr)
        Sbox = [i for i in range(256)]  # init sbox
        j = 0
        for i in range(A + 3): # A + 3 because we know the first 3 bytes from nonce
            j = (j + Sbox[i] + key[i % len(key)]) % 256
            Sbox[i], Sbox[j] = Sbox[j], Sbox[i]
            if i == 1:
                o0, o1 = Sbox[0], Sbox[1] # keep original 2 values to filter for swaps

        # Resolved condition
        i = A + 3
        if Sbox[1] < i and Sbox[1] + Sbox[Sbox[1]] == A + 3:
            if (o0 != Sbox[0] or o1 != Sbox[1]): # check for swaps
                continue
            key_byte = (keystream[0] - j - Sbox[i]) % 256 # first byte of the keystream is K3 = first byte of the key. Follow the equation
            probs[key_byte] += 1
    secret_decr.append(probs.index(max(probs))) # argmax from the array of probs
    print(bytes(secret_decr))**

ChaCha20-Poly1305

Introduce

ChaCha20: là một loại stream cipher tạo keystream 64 bytes mỗi block từ trạng thái 16 word 32-bit, thực hiện 20 rounds của phép Quarter-round.
Poly1305: MAC (one-time authenticator) tính tag 16 bytes dựa trên khóa 32 byte (chia thành r và s), hoạt động trên các block 16 byte, modulo prime $2^{130} - 5$.
ChaCha20-Poly1305 (AEAD): dùng ChaCha20 để sinh key một lần cho Poly1305, dùng ChaCha20 để mã hóa plaintext, rồi dùng Poly1305 để MAC cả AAD và ciphertext theo định dạng chuẩn — cho kết quả là ciphertext || 16-byte tag.

ChaCha20

ChaCha20 sử dụng một khóa 256-bit, none 96-bit và một counter 32-bit. Sinh ra một luồng keystream thành các block 64-byte (16 từ 32-bit).

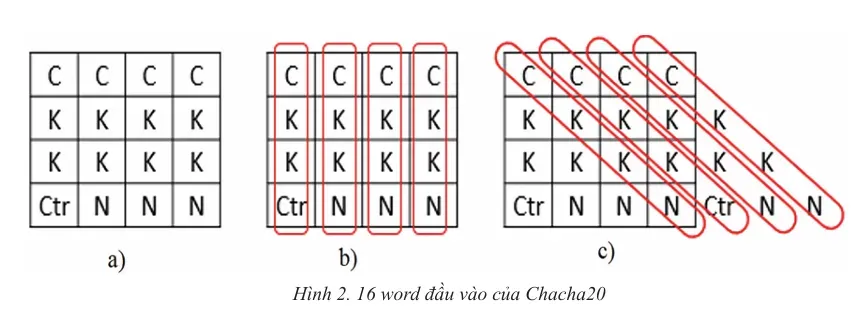
Cấu trúc của ChaCha20 là dùng một state gồm 16 words 32-bit (little-endian) sắp xếp theo chỉ số 0…15:

  
-------------------------
|  C  |  C  |  C  |  C  |        Các thông số: 128-bit hằng số C (4-word),
-------------------------                      256-bit khóa K (8-word),
|  K  |  K  |  K  |  K  |                      32-bit tham số bộ đếm Ctr (1-word),
-------------------------                      96-bit nonce N (3-word).
|  K  |  K  |  K  |  K  |
-------------------------
| Ctr |  N  |  N  |  N  |
-------------------------

Thực hiện 20 vòng lặp luân phiên thực thi các biến đổi dịch vòng cột (column round) theo hình 2b và dịch vòng chéo (diagonal round) theo hình 2c. Hai phép biến đổi dịch vòng này được thực thi chỉ nhờ một phép biến đổi QUARTERROUND.

  
def quarterround(a: int, b: int, c: int, d: int):
    a = (a + b) & 0xffffffff; d ^= a; d = rotl32(d, 16)
    c = (c + d) & 0xffffffff; b ^= c; b = rotl32(b, 12)
    a = (a + b) & 0xffffffff; d ^= a; d = rotl32(d, 8)
    c = (c + d) & 0xffffffff; b ^= c; b = rotl32(b, 7)
    return a, b, c, d

Trong 20 vòng lặp, mỗi vòng thực hiện 8 phép QUARTERROUND và thứ tự thực hiện như sau: QUARTERROUND từ 1 đến 4 thực hiện column round, còn QUARTERROUND từ 5 đến 8 thực hiện diagonal round. Đầu ra khối 20 vòng là 16-word, tiến hành cộng với 16-word đầu vào theo modulo $2^{32}$ để sinh 16-word khóa. Trong code mà mình để phía dưới, chỉ chạy 10 vòng lặp bởi vì trong mỗi vòng lặp ta dùng Double round = Column round + Diagonal round.

Bản rõ được xử lý trong quá trình mã hóa theo từng 512-bit (16 word), nếu bản rõ có độ dài không là bội của 512 thì sẽ được padding thêm các bit \x00 ở cuối.

Thuật toán ChaCha20 thực hiện gọi liên tiếp hàm khối ChaCha20 với cùng key, nonce và các tham số bộ đếm Ctr tăng dần liên tiếp. Sau đó xếp tuần tự trạng thái kết quả tạo một keystream có kích cỡ lớn hơn hoặc bằng với kích thước plaintext. Phép mã hóa thực hiện phép ciphertxt = plaintext XOR keystream . Quá trình giải mã được thực hiện bằng cách tương tự với đầu vào là bản mã thay vì bản rõ.

Code encrypt ChaCha20:

  
import struct

SIGMA = b"expand 32-byte k"

def rotl32(x: int, n: int) -> int:
    return ((x << n) | (x >> (32 - n))) & 0xffffffff

def le_bytes_to_words(b: bytes):
    if len(b) % 4 != 0:
        raise ValueError("byte length must be multiple of 4")
    return list(struct.unpack("<" + "I" * (len(b)//4), b))

def words_to_le_bytes(*words: int) -> bytes:
    return struct.pack("<" + "I" * len(words), *[(w & 0xffffffff) for w in words])

def quarterround(a: int, b: int, c: int, d: int):
    a = (a + b) & 0xffffffff; d ^= a; d = rotl32(d, 16)
    c = (c + d) & 0xffffffff; b ^= c; b = rotl32(b, 12)
    a = (a + b) & 0xffffffff; d ^= a; d = rotl32(d, 8)
    c = (c + d) & 0xffffffff; b ^= c; b = rotl32(b, 7)
    return a, b, c, d

def chacha20_block(key: bytes, counter: int, nonce: bytes, verbose: int = 0, pause: bool = False) -> bytes:
    if len(key) != 32 or len(nonce) != 12:
        raise ValueError("key=32B, nonce=12B required")
    k = le_bytes_to_words(key)
    n = le_bytes_to_words(nonce)
    const = le_bytes_to_words(SIGMA)
    state = [
        const[0], const[1], const[2], const[3],
        k[0], k[1], k[2], k[3], k[4], k[5], k[6], k[7],
        counter & 0xffffffff,
        n[0], n[1], n[2]
    ]
    w = state.copy()
    for _ in range(10):
		    # column round
        w[0], w[4], w[8],  w[12] = quarterround(w[0], w[4], w[8],  w[12])
        w[1], w[5], w[9],  w[13] = quarterround(w[1], w[5], w[9],  w[13])
        w[2], w[6], w[10], w[14] = quarterround(w[2], w[6], w[10], w[14])
        w[3], w[7], w[11], w[15] = quarterround(w[3], w[7], w[11], w[15])

        # diagonal round
        w[0], w[5], w[10], w[15] = quarterround(w[0], w[5], w[10], w[15])
        w[1], w[6], w[11], w[12] = quarterround(w[1], w[6], w[11], w[12])
        w[2], w[7], w[8],  w[13] = quarterround(w[2], w[7], w[8],  w[13])
        w[3], w[4], w[9],  w[14] = quarterround(w[3], w[4], w[9],  w[14])

    out_words = [(w[i] + state[i]) & 0xffffffff for i in range(16)]
    return words_to_le_bytes(*out_words)

def chacha20_keystream(key: bytes, initial_counter: int, nonce: bytes, length: int,
                       verbose: int = 0, pause: bool = False, demo_all_blocks: bool = False) -> bytes:
    blocks = []
    counter = initial_counter
    max_blocks = (1 << 32) - initial_counter
    needed_blocks = (length + 63) // 64
    if needed_blocks > max_blocks:
        raise ValueError("Message too long: 32-bit block counter would wrap.")
    for bi in range(needed_blocks):
        vrb = verbose if (demo_all_blocks or bi == 0) else 0
        blocks.append(chacha20_block(key, counter, nonce, verbose=vrb, pause=pause))
        counter = (counter + 1) & 0xffffffff
    return b"".join(blocks)[:length]

def chacha20_xor(key: bytes, counter: int, nonce: bytes, data: bytes,
                 verbose: int = 0, pause: bool = False, demo_all_blocks: bool = False) -> bytes:
    ks = chacha20_keystream(key, counter, nonce, len(data), verbose=verbose, pause=pause, demo_all_blocks=demo_all_blocks)
    return bytes([a ^ b for a, b in zip(ks, data)])

key = bytes.fromhex("1c9240a5eb55d38af333888604f6b5f0473917c1402b80099dca5cbc207075c0")
nonce = bytes.fromhex("000000000102030405060708")
plaintext = bytes.fromhex(
    "496e7465726e65742d4472616674732061726520647261667420646f63756d656e747320"
    "76616c696420666f722061206d6178696d756d206f6620736978206d6f6e74687320616e"
    "64206d617920626520757064617465642c207265706c616365642c206f72206f62736f6c"
    "65746564206279206f7468657220646f63756d656e74732e20506c656173652072656665"
    "7220746f2052616661656c2773202253656375726520486173682d6261736564204d6573"
    "736167652041757468656e7469636174696f6e222e"
)

counter = 1

ciphertext = chacha20_xor(key, counter, nonce, plaintext, verbose=False, pause=True)
print("Ciphertext (hex):", ciphertext.hex())

Poly1305

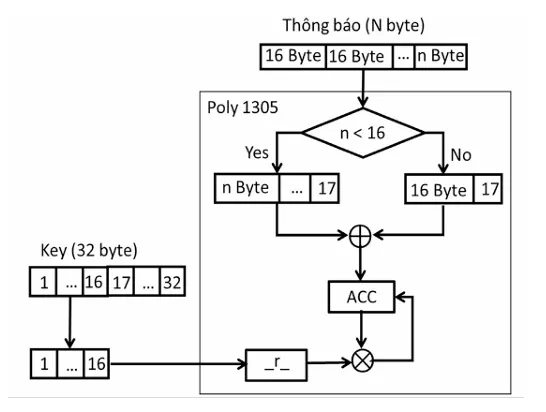
Poly1305 là cơ chế xác thực thông báo với đầu vào khóa 256-bit và một message có độ dài không cố định, đầu ra là một tag xác thực độ dài 128-bit. Tag Authentication này được bên nhận dùng để xác thực nguồn gốc của message.

Khóa đầu vào được chia thành 2 phần gọi là r và s , mỗi phân có độ dài 128-bit. Cặp (r, s) phải là duy nhất và không thể đoán được cho mỗi lần gọi. r cần được xử lý bằng bằng cách AND với 0x0ffffffc0ffffffc0ffffffc0fffffff.

(r, s) được tính bằng cách lấy 32-byte đầu của ChaCha20_block(key, counter = 0, nonce).

message đầu vào được chia thành các khối 16-byte (block cuối có thể ngắn hơn và sẽ được padding thêm các bit 0), các block 16-byte sẽ được đệm thêm vào 1 byte có giá trị 0x01 thành 17-byte, sau đó thực hiện một số phép tính với r để tạo một bộ tích lũy ACC (accumulator).

Công thức chi tiết ( $m_i$ là block thứ $i$ của message):

\[\text{acc} = 0 \\ \text{for each} \ m_i: \ \ \ \ \text{acc} = (\text{acc} + m_i) \cdot r \pmod {2^{130} - 5}\]

Cuối cùng:

\[\text{tag} = (\text{acc} + s) \pmod {2^{128}}\]

→ Đây chính là giá trị MAC 16-byte.

  
def poly1305_mac(msg: bytes, r_s: Tuple[bytes, bytes]) -> bytes:
    r_bytes, s_bytes = r_s
    if len(r_bytes) != 16 or len(s_bytes) != 16:
        raise ValueError("Poly1305 key must be 32 bytes split as 16+16 (r||s)")
    r_raw = int.from_bytes(r_bytes, "little")
    s = int.from_bytes(s_bytes, "little")
    r = r_raw & 0x0ffffffc0ffffffc0ffffffc0fffffff
    p = (1 << 130) - 5

    acc = 0
    for i in range(0, len(msg), 16):
        block = msg[i:i+16]
        n = int.from_bytes(block + b"\x01", "little")
        acc = (acc + n) % p
        acc = (acc * r) % p

    tag = (acc + s) % (1 << 128)
    return tag.to_bytes(16, "little")

ChaCha20-Poly1305

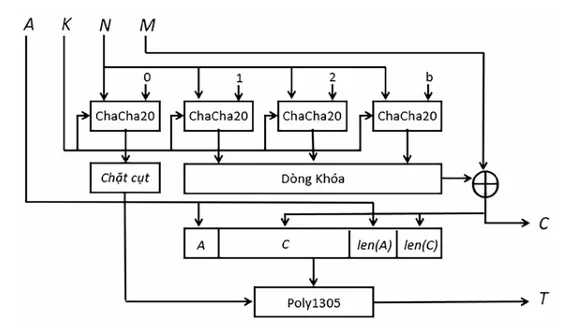
Tóm lại, ChaCha20-Poly1305 là hệ mã dòng có xác thực thông qua việc thực thi thuật toán mã hóa dòng ChaCha20 trong cơ chế xác thực Poly1305. Đầu vào của hệ mã dòng này là một khóa K dài 256-bit, một giá trị nonce N dài 96-bit, dữ liệu liên kết A có độ dài tùy ý, thông báo M có độ dài tùy ý. Đầu ra gồm 2 thành phần là bản mã C có cùng độ dài với bản rõ và thẻ xác thực T độ dài 128-bit.

Khóa dòng được sinh trong ChaCha20-Poly1305 bằng cách thực thi các hàm khối ChaCha20 với khóa K , giá trị nonce N và bộ đếm khởi tạo ban đầu có giá trị bằng 1. Khóa dòng sau đó được XOR với bản rõ để tạo bản mã C.

Thẻ xác thực được tính bởi cơ chế Poly1305 với khóa đầu vào là 256-bit đầu tiên, dữ liệu liên kết A , bản mã C và độ dài của A và C. Khóa đầu vào được tính bởi hàm khối ChaCha20 với khóa K , nonce N, bộ đếm có giá trị bằng 0 và được cắt còn 256-bit.

Cryptanalysis

Trong ChaCha20-Poly1305, thuật toán sinh ra keystream phụ thuộc vào (key, nonce, counter) . Nếu cùng (key, nonce) thì keystream của các block tương ứng sẽ trùng nhau giữa các message

→ Nếu 2 ciphertext mã hóa 2 plaintext khác nhau với cùng (key, nonce) thì keystream sẽ bị reuse.

Poly1305 dùng một one-time key (32 byte) được sinh ra từ ChaCha20 block với counter = 0 và cùng một nonce . Nếu nonce bị reuse, thì Poly1305 key r || s cũng bị reuse.

Cụ thể hơn, khi nonce được sử dụng lại, ta có 2 cặp (ct, tag) từ cùng một cặp (r, s) .

\[tag_1 = \text{Poly1305}(r, s, pad(ct_1)) = ((block_{1, 1} * r^i + block_{1, 2} * r^{i-1} + ... + block_{1, i} * r^1) \pmod {2^{130}-5}) + s \pmod {2^{128}} \\ tag_2 = \text{Poly1305}(r, s, pad(ct_2)) = ((block_{2, 1} * r^i + block_{2, 2} * r^{i-1} + ... + block_{2, i} * r^1) \pmod {2^{130}-5}) + s \pmod {2^{128}}\] \[\Rightarrow tag_1 - tag_2 = (r^i * A_1 + r^{i-1}*A_2 + ... + r^1 * A_i) \pmod {2^{130} - 5} \pmod {2^{128}}; \ \ \ \ \ A_i = (block_{1, i} - block_{2, i})\] \[\Rightarrow tag_1 - tag_2 = (r^i * A_1 + r^{i-1}*A_2 + ... + r^1 * A_i) + k * 2^{128} \pmod {2^{130} - 5} ; \ \ \ \ \ k \in [-4, 4]\]

Đến đây, ta chỉ cần bruteforce giá trị k rồi giải đa thức trên để tìm nghiệm r , sau đó tính lại s1, s2 tương ứng với tag1, tag2 xem nếu s1 == s2 thì chứng tỏ giá trị r đã đúng. Từ (r, s) ta có thể giả mạo tag cho bất kỳ tin nhắn nào bằng cách sử dụng keystream được tạo từ ChaCha20.

Cryptography

Stream cipher

This post is licensed under CC BY 4.0 by the author.

RC4

Introduce

Key Scheduling Algorithm

Pseudo Random Generation Algorithm

Cryptanalysis

KSA-based attacks (FMS attack)

ChaCha20-Poly1305

Introduce

ChaCha20

Poly1305

ChaCha20-Poly1305

Cryptanalysis

Trending Tags