WannaGame Championship 2025

Write-up for some challenges Cryptography

Posted Dec 10, 2025 Updated Dec 11, 2025

By Dang Minh Tu

17 min read

Vừa qua mình đã tham gia giải WannaGame Championship 2025, team mình laviaespa đã đạt top 4 bảng xếp hạng chung cuộc. Đây là các bài Cryptography mình đã làm được trong giải.

Linear 101

Source code:

  
import random
import os

n = 128
random.seed("Wanna Win?")

def encrypt(A, x):
    b = [0] * n
    for i in range(n):
        for j in range(n):
            b[i] = max(b[i], A[i][j] + x[j])
    return b

def game():
    for round in range(64):
        try:
            print(f"Round {round+1}/64")
            A = [random.randbytes(n) for _ in range(n)]
            x = os.urandom(128)
            b = encrypt(A, x)

            print(f"{b = }")
            sol = bytes.fromhex(input("x = "))
            if len(sol) != n:
                return False

            if encrypt(A, sol) != b:
                print("Wrong!")
                return False
        except:
            return False
    return True

if game():
    print(open("flag.txt", "r").read())
else:
    print("You lose...")

Bug lớn nhất ở trong bài này đó chính là việc tiết lộ cho ta biết seed của hàm random. Từ đó ta có thể sinh ra lại mảng A. Hàm encrypt(A, x) sẽ trả về một mảng b có n phần tử với b[i] = max(b[i], A[i][j] + x[j]). Tức là:

\[b_i = \text{max}_j(A_{ij}+x_j) \\ \Rightarrow A_{ij} + x_j \le b_i \\ \Rightarrow x_j \le b_i - A_{ij} \\ \Rightarrow x_j \le min_i(b_i - A_{ij}) \\ \Rightarrow x_j = min_i(b_i - A_{ij})\]

Vậy, ta đã có thể tạo được một mảng x thỏa mãn điều kiện encrypt(A, sol) == b. Solve script:

  
from pwn import *
import random, json

io = remote("challenge.cnsc.com.vn", 30429, level='debug')
N = 128

rand = random.Random()
rand.seed("Wanna Win?")
As = [[rand.randbytes(N) for _ in range(N)] for _ in range(64)]

def calc(A, b):
    x = [0] * N
    for j in range(N):
        m = 10**9
        for i in range(N):
            m = min(m, b[i] - A[i][j])
        x[j] = m % 256
    return bytes(x)

for r in range(64):
    io.recvuntil(b"b = ")
    b = json.loads(io.recvline().decode().strip())
    io.recvuntil(b"x = ")
    x = calc(As[r], b)
    io.sendline(x.hex())

print(io.recvall())

# W1{W3I1-l_THiNK_lts_3ASler_Than_nOrmAL-Lln3Ar_41gebra_problem0}

Boring Signing

Source code:

  
// gcc base85.c chall.c prime.c rsa.c -o chall -lcrypto
#include <stdio.h>
#include <string.h>
#include <stdint.h>
#include <ctype.h>
#include "prime.h"
#include "rsa.h"
#include "base85.h"

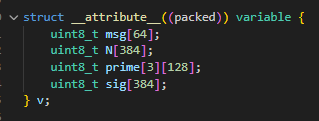
struct __attribute__((packed)) variable {
    uint8_t msg[64];
    uint8_t N[384];
    uint8_t prime[3][128];
    uint8_t sig[384];
} v;

int main() {
    setvbuf(stdout, NULL, _IONBF, 0);

    int choice;

    keygen(v.N, v.prime, 1024 * 3);
    printf("N = "); print_b85(v.N, sizeof(v.N));
    printf("\n");
    uint8_t target[64] = "1_d4r3_y0u_70_519n_7h15_3x4c7_51x7y_f0ur_by73_57r1n9_w17h_my_k3y";

    for (int i = 0; i <= 20; i++) {
        printf("Sign(0) or Verify(1): ");
        scanf("%d", &choice);

        int c;
        while ((c = getchar()) != '\n' && c != EOF);

        switch (choice)
        {
        case 0:
            printf("Input your message in base85:\n");
            input_b85(v.msg, 64);
            while ((c = getchar()) != '\n' && c != EOF);

            if (!memcmp(v.msg, target, 64)) {
                printf("Nuh uh\n");
                return 0;
            }
            sign(v.msg, v.N, v.prime, v.sig);
            printf("sig = "); print_b85(v.sig, sizeof(v.sig));
            printf("\n");
            break;
        case 1:
            printf("Provide your signature in base85:\n");
            uint8_t check[384];
            input_b85(check, 384);
            while ((c = getchar()) != '\n' && c != EOF);

            if (verify(target, check, v.N)) {
                uint8_t flag[64];
                FILE *f_flag = fopen("flag", "r");
                flag[fread(flag, 1, sizeof flag - 1, f_flag)] = 0;
                printf("%s\n", flag);
                fclose(f_flag);
                return 0;
            } else {
                printf("Wrong !\n");
                return 0;
            }
            break;
        default:
            printf("Huh ?\n");
            return 0;
        }
    }
}

Sau khi phân tích các file code của challenge thì mình nhận thấy rằng có một bug ở trong base85.c là hàm mã hóa và giải mã base85.

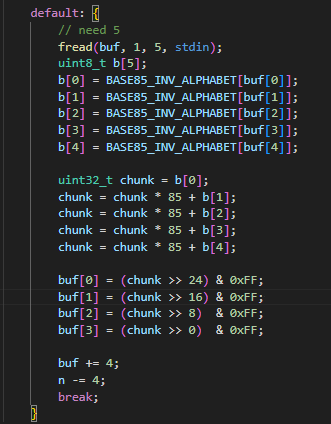
Hàm input_b85 sẽ nhận con trỏ buf làm nơi chứa dữ liệu sau khi giải mã base85. Trong giải mã base85 thì cứ 5 bytes input sẽ tạo thành 4 bytes output. Và trong code này author đã cố tình sử dụng trực tiếp buf để chứa dữ liệu từ stdin thông qua lệnh fread(buf, 1, 5, stdin);. Thì khi ta gọi input_b85(v.msg, 64), vòng lặp while sẽ xử lý mỗi lần 5 bytes input. Đến vòng lặp cuối cùng (n = 4): con trỏ buf đang trỏ đến v.msg[60] (là bytes thứ 61 của msg). Thì hàm fread(buf, 1, 5, stdin) sẽ đọc 5 bytes từ bàn phím và ghi vào bộ nhớ bắt đầu từ v.msg[60]. Khi đó:

Byte input 1 -> buf[0] -> v.msg[60]
Byte input 2 -> buf[1] -> v.msg[61]
Byte input 3 -> buf[2] -> v.msg[62]
Byte input 4 -> buf[3] -> v.msg[63]
Byte input 5 -> buf[4] -> v.msg[64] (buffer overflow)

Và nhìn vào struct được tạo trong file chall.c ta thấy:

Vì struct variable được định nghĩa với packed nên compiler sẽ không padding byte nào giữa các biến. Khi đó v.N sẽ nằm ngay sau v.msg, suy ra byte bị tràn sẽ là byte đầu tiên của N.

Tận dụng bug này, mình đã thử từng giá trị byte có thể (256 giá trị) để thay thế byte đầu tiên của N để tìm một giá trị N' sao cho N' là một số nguyên tố. Khi đó phi(N') = N' - 1 từ đó tính được d và ký cho target. Lí do làm như vậy là bởi vì hàm verify() đó sử dụng luôn giá trị N sau khi bị ghi đè.

Solve script:

  
from pwn import *
from Crypto.Util.number import bytes_to_long, long_to_bytes, isPrime, inverse
from hashlib import sha256
import base64

def solve():
    io = remote('challenge.cnsc.com.vn', 32730, level='debug')

    io.recvuntil(b"N = ")
    N_b85 = io.recvline().strip()
    N_bytes = base64.a85decode(N_b85)

    found_byte = None
    prime_N = 0

    for b in range(256):
        candidate_bytes = bytearray(N_bytes)
        candidate_bytes[0] = b
        candidate_N = bytes_to_long(candidate_bytes)

        if isPrime(candidate_N):
            found_byte = b
            prime_N = candidate_N
            break

    if found_byte is None:
        io.close()
        return None

    d = inverse(0x10001, prime_N - 1)

    target = b"1_d4r3_y0u_70_519n_7h15_3x4c7_51x7y_f0ur_by73_57r1n9_w17h_my_k3y"
    target = bytes_to_long(sha256(target).digest())

    sig_forged_int = pow(target, d, prime_N)

    io.sendlineafter(b"Sign(0) or Verify(1): ", b"0")

    payload = b'!!!!!' * 15 + b'!!!!' + bytes([found_byte])

    io.sendlineafter(b"base85: \n", payload)

    io.sendlineafter(b"Sign(0) or Verify(1): ", b"1")

    sig_bytes = long_to_bytes(sig_forged_int)
    if len(sig_bytes) < 384:
        sig_bytes = b'\x00' * (384 - len(sig_bytes)) + sig_bytes

    sig_payload = base64.a85encode(sig_bytes)
    io.sendlineafter(b"base85\n", sig_payload)

    result = io.recvline()
    if b"Wrong" in result or b"Huh" in result:
        return None

    return result

while True:
    flag = solve()
    if flag is not None:
        print(flag)
        break

# W1{I_ShOUlD-u53-PYTHon-t0-lmPI3M3n7-CRYp7O9rApHIC_SCH3M3S..8bf}

Interesting Signing

Source code:

  
// gcc base85.c chall.c prime.c rsa.c -o chall -lcrypto
#include <stdio.h>
#include <string.h>
#include <stdint.h>
#include <ctype.h>
#include "prime.h"
#include "rsa.h"
#include "base85.h"

struct __attribute__((packed)) variable {
    uint8_t msg[64];
    uint8_t N[384];
    uint8_t prime[3][128];
    uint8_t sig[384];
} v;

int main() {
    setvbuf(stdout, NULL, _IONBF, 0);

    int choice;

    keygen(v.N, v.prime, 1024 * 3);
    printf("N = "); print_b85(v.N, sizeof(v.N));
    printf("\n");
    uint8_t target[64] = "1_d4r3_y0u_70_519n_7h15_3x4c7_51x7y_f0ur_by73_57r1n9_w17h_my_k3y";

    for (int i = 0; i <= 20; i++) {
        printf("Sign(0) or Verify(1): ");
        scanf("%d", &choice);

        int c;
        while ((c = getchar()) != '\n' && c != EOF);

        switch (choice)
        {
        case 0:
            printf("Input your message in base85:\n");
            input_b85(v.msg, 64);
            while ((c = getchar()) != '\n' && c != EOF);

            if (!memcmp(v.msg, target, 64)) {
                printf("Nuh uh\n");
                return 0;
            }
            sign(v.msg, v.N, v.prime, v.sig);
            printf("sig = "); print_b85(v.sig, sizeof(v.sig));
            printf("\n");
            break;
        case 1:
            printf("Provide your signature in base85:\n");
            uint8_t check[384];
            input_b85(check, 384);
            while ((c = getchar()) != '\n' && c != EOF);

            if (verify(target, check, v.prime)) {
                uint8_t flag[64];
                FILE *f_flag = fopen("flag", "r");
                flag[fread(flag, 1, sizeof flag - 1, f_flag)] = 0;
                printf("%s\n", flag);
                fclose(f_flag);
                return 0;
            } else {
                printf("Wrong !\n");
                return 0;
            }
            break;
        default:
            printf("Huh ?\n");
            return 0;
        }
    }
}

Bài này là một phiên bản khó hơn rất nhiều so với bài trước khi đã cách check của hàm verify(), thay vì sử dụng giá trị N' đã bị ghi đè thì nó sẽ tính lại N ban đầu từ các giá trị p, q, r. Nhưng vì lí do như vậy, hướng đi duy nhất của ta sẽ là tìm cách recover p, q, r từ việc sử dụng sign() với N_fault. Bug base85 của bài Boring Signing vẫn được sử dụng trong bài này => Ta có thể thay đổi byte đầu tiên của N_origin theo ý của mình. Nhưng làm sao để recover p, q, r?

Trong lúc giải đang diễn ra, mình đã osint được một cái paper rất giống bài này chỉ khác ở chỗ trong paper nó sử dụng N = pq (còn bài này thì N = pqr). Paper này nói về cách attack chống lại RSA-CRT Signature. Cụ thể hơn:

Ta có: $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sigma_p = H(m)^d \pmod p, \ \ \ \ \sigma_q = H(m)^d \pmod q, \ \ \ \ \sigma_r = H(m)^d \pmod r$

Hàm sign() sẽ trả về chữ ký:

\[\sigma = \sigma_p \cdot \alpha + \sigma_q \cdot \beta + \sigma_r \cdot \theta \pmod N\]

Với:

\[\alpha = qr \cdot ((qr)^{-1} \mod p) \\ \beta = pr \cdot ((pr)^{-1} \mod q) \\ \theta = pq \cdot ((pq)^{-1} \mod r)\]

Và một chữ ký $\sigma’$ của cùng $H(m)$ được tính bởi modulo $N’$ (chỉ khác duy nhất byte MSB so với $N$).

\[\sigma' = \sigma_p \cdot \alpha + \sigma_q \cdot \beta + \sigma_r \cdot \theta \pmod {N'}\]

Thì khi ta CRT lên $\sigma, \sigma’$ sẽ được:

\[v = \sigma_p \cdot \alpha + \sigma_q \cdot \beta + \sigma_r \cdot \theta \pmod {N \cdot N'}\]

Vì $\sigma_p \cdot \alpha + \sigma_q \cdot \beta + \sigma_r \cdot \theta < 3N$ (mỗi số hạng đều bé hơn N), và $N \cdot N’ \approx N^2$ rất lớn, nên khi CRT thì giá trị $v$ chính xác là $\sigma_p \cdot \alpha + \sigma_q \cdot \beta + \sigma_r \cdot \theta$ (không bị modulo).

Khi đó $v$ chính là một tổ hợp tuyến tính của $\alpha, \beta, \theta$ trong $\mathbb{Z}$. Thuật toán của ta sẽ như sau:

Ban đầu lấy $l$ cặp $\sigma_i, \sigma’_i$ tương ứng là các chữ ký của message $m$ với modulo $N, N’$ ($m, N’$ thay đổi tùy ý với từng cặp).

Sau đó CRT từng cặp để tính ra giá trị $v_i = \text{CRT}_{N, N’}(\sigma_i, \sigma’_i)$ tương ứng.

Giả sử ta xét trên modulo $p$, ta có:

\[v \equiv \sigma_p \pmod p \\ \Rightarrow v = k \cdot p + \sigma_p\]

Với $\sigma_p$ (khoảng 1024 bit), $v$ (khoảng 6000 bit), $k$ (khoảng 5000 bit).

Ta đã lấy được $l$ giá trị $v_i$:

\[v_1 = k_1p + \sigma_{p, 1} \\ v_2 = k_2p + \sigma_{p, 2} \\ ... \\ v_l = k_lp + \sigma_{p, l} \\\]

Gọi vector $v = (v_1, v_2, …, v_l) \in \mathbb{Z}^l$. Bây giờ ta muốn tìm lại các giá trị $\sigma_{p,1},\sigma_{p,2},…,\sigma_{p,l}$. Mục đích là để ta có thể recover $p = \text{GCD}(\frac{v_i}{\sigma_{p,i}}, N)$.

Note: Nếu lattice $L$ và $L^{\perp}$ nằm trong cùng không gian $\mathbb{R}^n$ thì $\text{rank}(L) + \text{rank}(L^{\perp}) = n$.

Dùng thuật toán LLL để tìm một cơ sở ${ b_1, b_2, …, b_{l-1} }$ của lattice $v^{\perp} \subset \mathbb{Z}^{\ell}$ (lattice này có rank $l-1$) là những vector trực giao với $v$. Ta xây dựng ma trận như sau:

\[M_1 = \begin{pmatrix} Kv_1 & 1 & 0 & \cdots & 0 \\ Kv_2 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ Kv_l & 0 & 0 & \cdots & 1 \end{pmatrix}\]

Nếu ta chọn $K$ rất lớn, LLL sẽ ưu tiên tìm các vector có cột đầu tiên rất nhỏ (xấp xỉ 0). Khi đó, vector chứa các hệ số bên phải sẽ là một vector trong lattice $v^{\perp}$. Giả sử sau khi LLL ta tìm được một vector $c = (c_1, c_2, …, c_l) \in v^{\perp}$, khi đó:

\[\sum_{i=1}^{l} c_i \cdot v_i = 0 \\ \Rightarrow \sum_{i=1}^{l} c_i \cdot (k_ip + \sigma_{p,i}) = 0 \\ \Rightarrow \sum_{i=1}^{l} c_i \cdot k_ip + \sum_{i=1}^{l} c_i \cdot \sigma_{p,i} = 0 \\\]

Vì $k_ip$ rất lớn nên LLL sẽ cố gắng chọn những $c_i$ sao cho $\sum_{i=1}^{l} c_i \cdot k_ip$ nhỏ nhất có thể (tốt nhất là bằng 0). Khi đó ta sẽ có một ràng buộc cho lattice $v^{\perp}$ là $\sum_{i=1}^{l} c_i \cdot \sigma_{p,i} = 0$. Đây cũng chính là lí do tại sao $v^{\perp}$ có rank là $l-1$.

Sau đó, ta lấy $l-3$ vector ${ b_1, b_2, …, b_{l-3} }$ làm cơ sở cho lattice $L’ \subset \mathbb{Z}^l$ có rank là $l-3$ Ta xây dựng ma trận:

\[M_2 = \begin{pmatrix} K' b_{1,1} & \cdots & K' b_{l-2,1} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ K' b_{1,l} & \cdots & K' b_{l-2,l} & 0 & \cdots & 1 \end{pmatrix}\]

Khi đó, sử dụng LLL sẽ tìm được vector ngắn nhất $\sigma_p = (\sigma_{p,1}, \sigma_{p,2},…, \sigma_{p,l})$ (ở đây mình đang giả sử tính trên modulo $p$ thôi chứ thực ra có thể là $q, r$ bởi vì 3 giá trị đó độ lớn ngang nhau nên LLL sẽ không phân biệt được) của lattice $L’^{\perp}$ sao cho $\sigma_p \cdot b_i = 0$. Đây sẽ là các giá trị $\sigma_p$ mà ta cần tìm.

Giải thích tại sao lattice $L’$ lại có rank là $l-3$: Ban đầu ta có:

\[\langle c, v \rangle = 0 \Rightarrow \langle c, \sigma_p \cdot \alpha + \sigma_q \cdot \beta + \sigma_r \cdot \theta \rangle =0 \\ \Rightarrow \alpha \langle c, \sigma_p \rangle + \beta \langle c, \sigma_q \rangle + \theta \langle c, \sigma_r \rangle = 0\]

Vì $\alpha, \beta, \theta$ là các số rất lớn và độc lập tuyến tính trên $\mathbb{Z}$ nên phương trình này chỉ đúng khi và chỉ khi:

\[\langle c, \sigma_p \rangle = 0 \\ \langle c, \sigma_q \rangle = 0 \\ \langle c, \sigma_r \rangle = 0 \\\]

Giả sử $W = \text{span}(\sigma_p, \sigma_q, \sigma_r)$, vì 3 vector đó độc lập tuyến tính nên $\text{dim}(W) = 3$. Khi đó, $\text{dim}(W^{\perp}) = \text{dim}(\mathbb{Z}^l) - \text{dim}(W) = l - 3$. Đây chính là lattice $L’$ mà ta đã tìm được sau lần LLL đầu tiên.

Khi đã có được $\sigma_p$ rồi thì ta có thể recover $p = \text{GCD}(\frac{v_i}{\sigma_{p,i}}, N)$, tương tự với $q, r$.

Sau khi đã recover được $p, q, r$ thì việc còn lại rất đơn giản là tạo $\phi(N), d$ sau đó ký target rồi gửi chữ ký đó cho server và lấy flag.

Solve script:

  
from pwn import *
from hashlib import sha256
import base64
from Crypto.Util.number import *
from sage.all import *
import os
import itertools

while True:
    io = remote('challenge.cnsc.com.vn', 30289, level='debug')
    io.recvuntil(b"N = ")
    N_bytes = base64.a85decode(io.recvline().strip())
    N = bytes_to_long(N_bytes)

    def sign(payload):
        io.sendlineafter(b"Sign(0) or Verify(1): ", b"0")
        io.sendlineafter(b"base85:\n", payload)
        sig = io.recvline().strip().decode().split(' = ')[1]
        return bytes_to_long(base64.a85decode(sig))

    sig_1, sig_2, N_fault = [], [], []
    NUM_SAMPLES = 9
    MSG = [b'!', b'@', b'#', b'$', b'%', b'^', b'&', b'*', b'(', b')']

    for b in range(NUM_SAMPLES):
        payload = MSG[b] * 79 + bytes([N_bytes[0]])
        sig_1.append(sign(payload))

    for b in range(NUM_SAMPLES):
        payload = MSG[b] * 79 + bytes([b + 1])
        sig_2.append(sign(payload))

        N_fault.append(bytes([b + 1]) + N_bytes[1:])
    N_fault = [bytes_to_long(nf) for nf in N_fault]

    v = []
    for i in range(NUM_SAMPLES):
        val = crt([sig_1[i], sig_2[i]], [N, N_fault[i]])
        v.append(val)

    num_primes = 3
    num_ortho = NUM_SAMPLES - num_primes

    K1 = 2 * N
    dim1 = NUM_SAMPLES + 1
    base1 = []

    for i in range(NUM_SAMPLES):
        vec = [0] * dim1
        vec[0] = K1 * v[i]
        vec[i + 1] = 1
        base1.append(vec)

    M1 = Matrix(ZZ, base1)
    print("Running LLL 1...")
    reduced1 = M1.LLL()

    ortho_vecs = []
    for i in range(num_ortho):
        row = list(reduced1[i])
        ortho_vecs.append(row[1:])

    K2 = 2**(1024 * 2)
    base2 = []

    for i in range(NUM_SAMPLES):
        vec = []
        for j in range(num_ortho):
            vec.append(K2 * ortho_vecs[j][i])

        for j in range(NUM_SAMPLES):
            if i == j: vec.append(1)
            else: vec.append(0)
        base2.append(vec)

    M2 = Matrix(ZZ, base2)
    print("Running LLL 2...")
    reduced2 = M2.LLL()

    print(reduced2[0])
    exit()

    found_factors = set()

    w_candidates = []
    rows_to_check = min(reduced2.nrows(), 10)
    for r_idx in range(rows_to_check):
        val = reduced2[r_idx][num_ortho]
        w_candidates.append(val)

    import itertools
    coeffs = [-1, 0, 1]
    combinations = list(itertools.product(coeffs, repeat=min(len(w_candidates), 3)))

    for combo in combinations:
        if all(c==0 for c in combo): continue

        w_guess = sum(c*w for c, w in zip(combo, w_candidates[:3]))

        vals_to_check = [v[0] - w_guess, v[0] + w_guess]

        for val in vals_to_check:
            factor = gcd(val, N)
            if factor > 1 and factor < N:
                found_factors.add(factor)

    final_primes = set()

    candidates = list(found_factors)
    for f in found_factors:
        candidates.append(N // f)

    for i in range(len(candidates)):
        for j in range(i + 1, len(candidates)):
            g = gcd(candidates[i], candidates[j])
            if g > 1:
                if is_prime(g): final_primes.add(g)
                if is_prime(candidates[i] // g): final_primes.add(candidates[i] // g)
                if is_prime(candidates[j] // g): final_primes.add(candidates[j] // g)

    for f in candidates:
        if is_prime(f): final_primes.add(f)

    sorted_primes = sorted(list(final_primes))
    if len(sorted_primes) == 3:
        p = sorted_primes[0]
        q = sorted_primes[1]
        r = sorted_primes[2]

        print(f"p = {p}")
        print(f"q = {q}")
        print(f"r = {r}")

        if p * q * r == N:
            print("Recover Success !!!")

        phi = (p - 1) * (q - 1) * (r - 1)
        e = 0x10001
        d = inverse(e, phi)

        target = b"1_d4r3_y0u_70_519n_7h15_3x4c7_51x7y_f0ur_by73_57r1n9_w17h_my_k3y"
        target = bytes_to_long(sha256(target).digest())
        sig = pow(target, d, N)

        sig_bytes = long_to_bytes(sig)
        if len(sig_bytes) < 384:
            sig_bytes = b'\x00' * (384 - len(sig_bytes)) + sig_bytes
        sig_payload = base64.a85encode(sig_bytes)

        io.sendlineafter(b"Sign(0) or Verify(1): ", b"1")
        io.sendlineafter(b"base85:\n", sig_payload)

        io.recvline()

        exit()

    io.close()

# W1{M@Y63_1-AM_NOt-@_G0oD-D3veIopeR...cf716}

Cryptography

Lattice RSA

This post is licensed under CC BY 4.0 by the author.

Linear 101

Boring Signing

Interesting Signing

Trending Tags